Informações Gerais
Nesta disciplina nós aprendemos as técnicas clássicas para a manipulação algorítmica de grafos.
Informações importantes sobre a disciplina – como justificativa, objetivos, ementa e bibliografia – podem ser encontrados na regulamentação oficial.
O nosso livro de referência é o "Cormen", que contém tudo o que veremos e muito mais. Ele e outros livros pelos quais o assunto da disciplina pode ser estudado estão listados tanto na bibliografia desta página quanto na regulamentação da disciplina.
Todas as atividades da disciplina já têm data estimada no plano de atividades. Se você percebeu um choque de datas importantes com outra disciplina, ou se você já sabe que não poderá fazer uma das nossas provas na data prevista, por favor me comunique o quanto antes!
Esteja atento, desde o início do semestre, às regras para solicitação de segunda chamada e para o cálculo da nota da disciplina.
Sugestões para conseguir um bom desempenho na disciplina:
Acompanhe as aulas com atenção.
Se uma dúvida surgir durante a aula, tire-a imediatamente.
Faça os exercícios essenciais a cada aula (são 2 por aula).
Se precisar, você também pode me contactar fora do horário de aula.
Regras
-
Segunda chamada: consulte as regras para a solicitação de prova de segunda chamada.
-
Nota da disciplina:
Consistirá na média aritmética das notas obtidas pelo aluno
nas 5 avaliações parciais da disciplina:
Média das APs ≥ 7 7 > média ≥ 4 < 4 Situação Aprovado AF Reprovado
Bibliografia
O livro de referência da disciplina é o "Cormen": ele contém tudo o que estudaremos e muito mais (não haverá, porém, compromisso em seguir linearmente livro algum).
Original: Introduction to Algorithms (third edition). Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein. MIT Press. 2009. ISBN: 9780262033848 (capa dura) e 9780262533058 (capa fina).
Tradução: Algoritmos – Teoria e Prática. Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein. Editora Campus. 2012. ISBN: 978-85-352-3699-6.
Estes outros livros também cobrem todo o conteúdo ou boa parte dele:
Algoritmos. Sanjoy Dasgupta, Christos Papadimitriou, Umesh Vazirani. McGraw-Hill. 2009. ISBN: 978-85-7726-032-4.
Algorithms. Sanjoy Dasgupta, Christos Papadimitriou, Umesh Vazirani. McGraw-Hill. 2006. ISBN: 978-0-07-352340-8.
Projeto de Algoritmos – com implementações em Pascal e C - 3ª edição. Nivio Ziviani. Cengage Learning. 2011. ISBN: 9788522110506.
Veja o capítulo 7.
Algorithms, 4th Edition . Robert Sedgewick, Kevin Wayne. Addison-Wesley. 2011. ISBN: 978-0-321-57351-3.
Veja o capítulo 4.
Algorithm Design and Applications. Michael T. Goodrich, Roberto Tamassia. Wiley. 2015. ISBN: 978-1-118-33591-8.
Veja a Parte 4. Além disso, da versão de 2002 desse livro, há um capítulo sobre grafos publicamente acessível.
Plano de Atividades
A disciplina possui 34 encontros planejados, sendo 27 aulas (19 teóricas e 8 práticas), 5 avaliações parciais e uma avaliação final que poderá ser dividida em 2 dias. Abaixo estão as datas e descrições de cada encontro, sendo importante ressaltar que, nos dias de prova, a ideia é aplicar a prova na primeira metade da aula e em seguida já apresentar as soluções das questões:
| 2016 | ||
|---|---|---|
| Aula | Data | Descrição |
| 01 | 17/08 | Introdução; Definições Básicas sobre Grafos. |
| 22/08 | (SEM AULA) Semana Acadêmica da Computação | |
| 24/08 | (SEM AULA) Semana Acadêmica da Computação | |
| 02 | 29/08 | Estruturas de Dados para Grafos; Problemas Simples. |
| 03 | 31/08 | Aula Prática: Detecção de Sumidouro Universal |
| 04 | 03/09 | (REPOSIÇÃO) Distância em Grafos Não-Ponderados; Percurso em Largura. |
| 05 | 03/09 | (REPOSIÇÃO) Aula Prática: Determinação das Componentes Conexas |
| * | 05/09 | AP1 + Soluções |
| 07/09 | (SEM AULA) Feriado da Independência do Brasil | |
| 06 | 09/09 | (REPOSIÇÃO) Corretude do Percurso em Largura |
| 07 | 12/09 | Detecção de Circuitos; Percurso em Profundidade. |
| 08 | 14/09 | Aula Prática: Detecção de Circuitos |
| 09 | 19/09 | Corretude do Percurso em Profundidade |
| 10 | 21/09 | Ordenação Topológica |
| * | 26/09 | AP2 + Soluções |
| 11 | 28/09 | Árvore Geradora Mínima (AGM): Problema, 1ª Estratégia e Corretude. |
| 12 | 03/10 | Algoritmo de Kruskal e Conjuntos Disjuntos |
| 13 | 05/10 | Detalhamento do Algoritmo de Kruskal |
| 14 | 10/10 | 2ª Estratégia para AGM: Corretude. |
| 12/10 | (SEM AULA) Feriado de N. S. Aparecida | |
| 15 | 17/10 | Algoritmo de Prim. |
| 16 | 19/10 | Aula Prática: Implementação de AGM |
| * | 24/10 | AP3 + Soluções |
| 17 | 26/10 | Caminhos Mínimos com Fonte Única: Problema e Discussão |
| 18 | 31/10 | Algoritmo de Dijkstra e Corretude |
| 02/11 | (SEM AULA) Feriado de Finados | |
| 19 | 07/11 | Algoritmo Bellman-Ford |
| 20 | 09/11 | Caminhos Mínimos em DAGs |
| 21 | 12/11 | (REPOSIÇÃO) Aula Prática: Implementação de Caminhos Mínimos. |
| * | 14/11 | AP4 + Soluções |
| 16/11 | SEM AULA: Sem alunos. | |
| 21/11 | Aulas Interrompidas, acompanhando as Greves Docente e Discente. | |
| 26/12 | Divulgado o Calendário de Reposição para 2016.2 | |
| 2017 | ||
| Aula | Data | Descrição |
| 04/01 | – | |
| 09/01 | – | |
| 22 | 11/01 | Fluxo em Grafos: Problema e Ideias de Solução. |
| 23 | 16/01 | Prova de Resultados sobre Fluxo |
| 24 | 18/01 | Complexidade do Método de Ford-Fulkerson |
| 25 | 23/01 | Complexidade do Algoritmo de Edmonds-Karp |
| 26 | 25/01 | Emparelhamento Máximo em Grafos Bipartidos |
| 27 | 30/01 | Aula Prática: Implementação de Fluxo Máximo. |
| * | 01/02 | AP5 + Soluções |
| * | 06/02 | AF – Parte 1 |
| * | 08/02 | AF – Parte 2 |
| * | 09/02 | Resultados Finais |
Aulas e Exercícios
Aqui estão os assuntos e exercícios das aulas que já aconteceram:
-
Aula 01 (2016-08-17, Segunda-feira):
-
Introdução à disciplina: conteúdo, página, avaliações, regras, etc.
-
Definições básicas sobre grafos – veja o material [1] abaixo.
-
Exemplos de manipulação matemática de grafos:
-
Prova de que Σv ∈ V d(v) = 2*|E| para todo grafo não-direcionado G = (V,E).
-
Prova de que, se existe um passeio de "u" a "v", então existe também um caminho de "u" a "v".
-
EXERCÍCIOS ESSENCIAIS:
-
Em sala, nós relacionamos, para um grafo não-direcionado qualquer, o número de arestas do grafo com os graus dos vértices do grafo. Entretanto, como fica essa relação no caso de grafos direcionados? Enuncie um resultado correspondente e prove-o precisamente, como fizemos em sala.
-
Suponha que você vai armazenar um mapa num computador. Mais precisamente, as informações do mapa que você pretende armazenar são apenas as seguintes:
-
Os nomes das cidades (no máximo 50 caracteres).
-
Que cidades estão diretamente ligadas por meio de uma estrada (isto é, sem cidades intermediárias), e o nome da estrada que as conecta (algo como "BR-116", de até 10 caracteres).
-
Que cidades estão diretamente ligadas a Fortaleza?
-
Que pares de cidades estão diretamente ligadas pela BR-116?
-
EXERCÍCIOS ADICIONAIS:
-
Prove que, se todos os vértices de um certo grafo não-direcionado têm grau > 1, então o grafo é cíclico, isto é, ele possui um ciclo.
Escreva um algoritmo para responder ao segundo tipo de consulta do exercício essencial 2 acima.
MATERIAIS DE ESTUDO:
-
Aqui está [1] um apanhado de definições que utilizaremos na disciplina (eu pretendo atualizar a lista sempre que necessário).
-
Esta nota de aula [2] introduz de maneira interessante o conceito de grafo e algumas aplicações – mas esteja atento a algumas diferenças na terminologia!
-
No Cormen, as definições básicas sobre grafos estão nas seções B.4 e B.5.
-
-
Aula 02 (2016-08-29, Segunda-feira):
- Representação de Grafos por Matriz de Adjacência.
- Representação de Grafos por Listas de Adjacência.
- Exercício em Sala: Algoritmos para Imprimir Vizinhos do Vértice "i".
EXERCÍCIOS ESSENCIAIS:
-
Escreva um algoritmo que receba um grafo não-direcionado G e índices "i" e "j", e que informe, retornando 1 ou 0, se os graus dos vértices "i" e "j" são iguais.
Seguindo o que fizemos em sala, você deve escrever 3 versões do algoritmo:
- Uma usando matriz de adjacência.
- Uma usando listas de adjacência.
- Uma independente da representação.
Além disso, você deve informar, usando a notação assintótica Θ, o tempo de execução das versões acima.
-
Escreva, de forma independente da representação do grafo, um algoritmo que receba como entrada um grafo direcionado G, e que informe se G possui um "sumidouro universal", isto é, um vértice do qual não há nenhuma aresta saindo, mas que tem arestas chegando de todos os outros vértices do grafo; se o grafo possuir tal vértice, o índice do vértice deve ser retornado; em caso contrário, o algoritmo deve retornar −1.
Além disso, responda: para alguma das 2 representações de grafo vistas na aula, o seu algoritmo executa em tempo linear sobre o tamanho grafo, isto é, em tempo O(|V| + |E|)?
EXERCÍCIOS ADICIONAIS:
-
Escreva um algoritmo que receba um grafo não-direcionado G, e que informe se G é ou não um grafo "completo", isto é, se G é tal que existe aresta entre todos os seus pares de vértices. Faça 3 versões do algoritmo: uma para matriz de adjacência, outra para listas de adjacência e outra independente da representação.
Escreva, de forma independente da representação do grafo, um algoritmo que receba um grafo não-direcionado G, além de índices de vértices "i" e "j", e que responda se há em G um caminho de "i" a "j" de tamanho no máximo 2. Além disso, qual é o tempo (assintótico) de execução do seu algoritmo, em cada uma das 2 representações que vimos?
MATERIAIS DE ESTUDO:
-
No Cormen, Matrizes e Listas de Adjacência são explicadas na seção 22.1.
-
Aula 03 (2016-08-31, Quarta-feira):
- Implementação sobre Representação e Manipulação Básica de Grafos.
INSTRUÇÕES PRELIMINARES:
-
O sistema operacional e a linguagem de programação ficam à sua escolha. A minha sugestão, porém, é o sistema Ubuntu e a linguagem C, que eu sempre utilizo e portanto poderei explicar com facilidade.
-
A seção sobre C do sítio cppreference.com fornece informações completas sobre a declaração e o funcionamento das funções da biblioteca padrão da linguagem C.
-
Mantenha sempre em mente que o objetivo da aula é concluir as tarefas propostas, e que isso deve ser feito durante o tempo de aula. Assim, seja objetivo ao programar: prefira soluções simples e faça pouco tratamento de erros, lembrando que você pode refinar o seu código depois da aula se assim desejar.
-
Eu estarei à disposição para ajudar: tire as suas dúvidas rapidamente, mesmo que sejam trivialidades de programação cuja solução você não esteja lembrando.
EXERCÍCIOS ESSENCIAIS:
-
Sumidouro Universal
-
Tarefa:
-
Você deverá escrever um programa que leia grafos direcionado e então informe se eles possuem ou não um sumidouro universal.
-
Cada grafo será lido de um arquivo de texto e deverá ser armazenado na memória por meio de Listas de Adjacência.
-
Os detalhes de como a entrada será lida seguem abaixo, assim como uma sugestão de roteiro a ser seguido na implementação.
-
-
Sugestão de Passos a Realizar:
-
Defina as estruturas (registros) que você vai precisar para representar grafos por meio de listas de adjacência.
Uma maneira de fazer isso é definir 2 estruturas:
-
Uma para os nós das listas de adjacência.
-
Outra para o grafo, contendo um ponteiro para o vetor de vértices e um inteiro para gravar o número de vértices.
Observação: esta estrutura em princípio seria dispensável, mas é conveniente definí-la já que na linguagem C um vetor não armazena o próprio tamanho.
-
-
Escreva uma função que receba o nome de um arquivo de texto, leia o grafo nele armazenado, armazene-o por Listas de Adjacência e retorne um ponteiro para o grafo assim armazenado.
Sugestão: escreva essa função agora; o formato dos arquivos de entrada é explicado abaixo.
-
Escreva uma função que receba um grafo, armazenado por listas de adjacência, e informe se ele possui ou não um sumidouro universal.
-
Utilizando as funções acima, escreva um programa que, para cada grafo da entrada:
-
Leia o grafo a partir do arquivo.
-
Descubra se ele possui ou não um sumidouro universal.
-
Compare a resposta obtida com a solução fornecida para o grafo.
-
Imprima na tela a resposta e se ela é igual à solução.
-
-
-
Formato dos Arquivos de Entrada: os grafos serão informados por meio de arquivos de texto no seguinte formato:
dl format=edgelist1 n=3 data: 1 2 1 3 2 3 3 1
Acima, a linha "n=3" informa que se trata de um grafo com 3 vértices, e as últimas quatro linhas informam as arestas do grafo. Observe que a numeração dos vértices começa em 1!Para o caso de você estar curioso, o formato acima foi escolhido porque (1) ele é bastante simples (existem formatos muito mais extensos), e (2) ele é reconhecido pela ferramenta Gephi, que nos permite visualizar grafos com facilidade.
DICA: um arquivo no formato acima pode ser facilmente lido por um código como:
FILE *arq = fopen(nome_arq, "r"); int n, u, v; fscanf(arq, "dl\nformat=edgelist1\nn=%d\ndata:\n", &n); ... // Criar grafo de "n" vértices while ( fscanf(arq, "%d %d", &u, &v) == 2 ) { ... // inserir aresta (u,v) } // while fclose(arq); -
Arquivos de Entrada: este arquivo contém os grafos de entrada (exemplo:
0_grafo.txt), e este arquivo contém as soluções (exemplo:0_solucao.txt).
-
-
Aula 04 (2016-09-03, Sábado (Reposição), às 08:30, no Bloco 952, Sala 2):
-
Problemas resolvíveis por um percurso linear da lista dos vértices e/ou arestas de um grafo.
-
Contar as arestas de um grafo não-direcionado.
-
-
Um problema mais elaborado: calcular a distância de "u" a "v" em G (não-direcionado).
-
Construção guiada da solução.
-
-
Problema relacionado: contar as componentes conexas de um grafo não-direcionado.
-
Ideias de solução do problema.
-
Escrita de um algoritmo.
-
EXERCÍCIOS ESSENCIAIS:
-
Escreva um algoritmo que, ao invés de retornar o tamanho de um caminho mínimo (distância) de "u" a "v", imprima na tela um tal caminho.
-
Suponha que desejamos rotular os vértices de um certo grafo não-direcionado como "bons" ou "maus", de forma que todas as arestas do grafo conectem um vértice "bom" a um vértice "mal". Em outras palavras, desejamos rotular os vértices de forma que nenhuma aresta conecte dois vértices de mesmo rótulo.
Para alguns grafos, é possível obter uma rotulação do tipo acima; para outros, isso não é possível (por exemplo se o grafo for completo e tiver mais de 2 vértices).
Assim sendo, escreva um algoritmo que receba como entrada um grafo não-direcionado e que responda se esse grafo admite uma rotulação do tipo acima.
EXERCÍCIOS ADICIONAIS:
-
Escreva uma variação do algoritmo de distância escrito em sala, usando 2 listas ao invés de 1 fila.
Escreva um algoritmo para calcular o tamanho da maior componentes conexa de um grafo não-direcionado.
MATERIAIS DE ESTUDO:
-
No Cormen, o Percurso em Largura é explicado na seção 22.2.
-
-
Aula 05 (2016-09-03, Sábado (Reposição), às 10h):
- Implementação: Determinar as Componentes Conexas.
INSTRUÇÕES PRELIMINARES:
-
O sistema operacional e a linguagem de programação ficam à sua escolha. A minha sugestão, porém, é o sistema Ubuntu e a linguagem C, que eu sempre utilizo e portanto poderei explicar com facilidade.
-
A seção sobre C do sítio cppreference.com fornece informações completas sobre a declaração e o funcionamento das funções da biblioteca padrão da linguagem C.
-
Mantenha sempre em mente que o objetivo da aula é concluir as tarefas propostas, e que isso deve ser feito durante o tempo de aula. Assim, seja objetivo ao programar: prefira soluções simples e faça pouco tratamento de erros, lembrando que você pode refinar o seu código depois da aula se assim desejar.
-
Eu estarei à disposição para ajudar: tire as suas dúvidas rapidamente, mesmo que sejam trivialidades de programação cuja solução você não esteja lembrando.
TAREFAS:
-
Componentes Conexas
-
TAREFA: Escreva um programa que determine as componentes conexas dos grafos de entrada desta questão, e que então compare as respostas obtidas com as soluções aqui fornecidas.
-
ENTRADA: neste arquivo (são 120 grafos e o relatório de geração), no mesmo formato combinado anteriormente, mas ATENÇÃO: embora os grafos sejam não-direcionados, cada aresta aparece apenas uma vez no arquivo!
-
SOLUÇÕES: neste arquivo, no seguinte formato:
-
A primeira linha contém os vértices, ordenados por número, da componente conexa do vértice 1 (como antes, os vértices foram numerados a partir de 1, para evitar diferença em relação aos arquivos de entrada).
-
Cada uma das outras linhas contém os vértices (ordenados) da componente conexa do vértice de menor rótulo que não tenha aparecido nas componentes listadas em linhas anteriores.
-
-
-
Aula 06 (2016-09-09, Sexta-feira (Reposição)):
-
Argumentação Intuitiva da Corretude do Percurso em Largura:
====================================================================== Algoritmo: distância Entrada: Um grafo não-direcionado G = (V,E) e vértices u,v ∈ V. Saída: Um inteiro. ---------------------------------------------------------------------- 01. PARA cada i ∈ V 02. | d[i] := −1 03. d[u] := 0 04. F := criar_fila_vazia() 05. inserir_em(u,F) 06. ENQUANTO !está_vazia(F) 07. | i := remover_primeiro(F) 08. | PARA cada j ∈ N(i) 09. | | SE d[j] = −1 10. | | | d[j] := d[i] + 1 11. | | | inserir_em(j,F) 12. RETORNE d[v]. ======================================================================
-
Estratégia de Prova de Corretude via Invariantes de Laço.
-
Descoberta e Prova de Invariantes para o Algoritmo (só o 1º foi provado em sala):
-
∀x ∈ V, d[x] é inteiro e [ d[x] != −1 → d[x] = δ(u,x) ].
-
∀x ∈ F, d[x] != −1.
-
∀x ∈ V, se d[x] != −1, então OU x ∈ F OU x ∉ F e, ∀y ∈ N(x), d[y] != −1.
-
Se F não está vazia e um vértice "h" é o primeiro de F, então, ∀x ∈ V, se δ(u,x) ≤ d[h], d[x] != −1.
-
Em F, se um vértice "x" vem antes de um vértice "y", então d[x] ≤ d[y] ≤ d[x] + 1.
-
Se F está vazia, então, ∀x ∈ V, se δ(u,x) != infinito, então d[x] != −1.
-
Não há vértices repetidos em F.
-
EXERCÍCIOS ESSENCIAIS:
-
Pressupondo que os invariantes acima já foram provados, prove que, se o algoritmo retorna um valor, então esse valor é de fato a distância de "u" a "v" (ou, se retorna −1, que essa distância é infinita).
-
Prove os invariantes 2 e 3 acima (você pode supor que os outros invariantes já foram provados).
EXERCÍCIOS ADICIONAIS:
-
Prove o invariante 5 acima (você pode supor os demais invariantes).
Prove o invariante 6 acima (você pode supor os demais invariantes).
MATERIAIS DE ESTUDO:
-
No Cormen, o conceito de invariante de laço é apresentado na seção 2.1, e a corretude do Percurso em Largura é provada (sem invariantes) na seção 22.2.
-
Estas notas de aula [1] [2] explicam como provar a corretude de algoritmos iterativos por meio de invariantes de laço. Esta nota de aula [3] explica como provar a terminação de laços utilizando o conceito de variante de laço.
-
-
Aula 07 (2016-09-12, Segunda-feira):
-
Detecção de Ciclos em Grafos Não-Direcionados (Percurso em Largura): Algoritmo, Tempo de Execução e Corretude.
-
Detecção de Circuitos em Grafos Direcionados: Concepção de Algoritmo via Percurso em Profundidade.
CORREÇÃO: no cálculo do tempo de execução do algoritmo de detecção de ciclos, eu acredito ter escrito ϴ(n + m), sendo n = |V| e m = |E|: por favor corrijam para O(n + m), já que o algoritmo pode detectar um ciclo e retornar antes de percorrer todo o grafo. Veja também a aula 10, na qual observamos que, embora o limite O(n + m) esteja correto, na verdade é possível argumentar que o algoritmo executa em O(n)!
EXERCÍCIOS ESSENCIAIS:
-
O nosso algoritmo de detecção de circuitos utilizou uma função recursiva para facilitar a expressão da ordem em que os vértices devem ser visitados e em que os seus estados devem ser alterados.
Escreva agora uma versão alternativa do algoritmo, que utilize uma pilha explícita ao invés de uma função recursiva.
Escreva uma variação do algoritmo escrito em sala, o qual não apenas informe se existe ou não um circuito no grafo de entrada, mas que também imprima um circuito na tela caso exista um.
EXERCÍCIOS ADICIONAIS:
-
Usando o percurso em profundidade, escreva um algoritmo que determine as componentes conexas de um grafo, gravando em comp[u] o número da componente conexa de "u", ∀u ∈ V.
-
Em quanto tempo executa o algoritmo de detecção de circuitos? Argumente também que ele é correto, em termos semelhantes àqueles que utilizamos ao discutir a corretude do algoritmo de detecção de ciclos.
MATERIAIS DE ESTUDO:
-
No Cormen, o Percurso em Profundidade é apresentado na seção 22.3.
-
-
Aula 08 (2016-09-14, Quarta-feira):
- Implementação: Detectar Circuitos em Grafos Direcionados.
INSTRUÇÕES PRELIMINARES:
-
O sistema operacional e a linguagem de programação ficam à sua escolha. A minha sugestão, porém, é o sistema Ubuntu e a linguagem C, que eu sempre utilizo e portanto poderei explicar com facilidade.
-
A seção sobre C do sítio cppreference.com fornece informações completas sobre a declaração e o funcionamento das funções da biblioteca padrão da linguagem C.
-
Mantenha sempre em mente que o objetivo da aula é concluir as tarefas propostas, e que isso deve ser feito durante o tempo de aula. Assim, seja objetivo ao programar: prefira soluções simples e faça pouco tratamento de erros, lembrando que você pode refinar o seu código depois da aula se assim desejar.
-
Eu estarei à disposição para ajudar: tire as suas dúvidas rapidamente, mesmo que sejam trivialidades de programação cuja solução você não esteja lembrando.
TAREFAS:
-
Detectar Circuitos
-
TAREFA: Escreva um programa que determine, para cada grafo de entrada desta questão, se ele possui ou não circuitos, e que então compare as respostas obtidas com as soluções aqui fornecidas.
-
ENTRADA: neste arquivo (são 160 grafos e o relatório de geração), no mesmo formato combinado anteriormente.
-
SOLUÇÕES: neste arquivo, no seguinte formato:
-
A primeira linha informa, por 1 ou 0, se há circuitos.
-
Se houver circuitos, a 2ª linha dá exemplo de um.
-
-
-
Aula 09 (2016-09-19, Segunda-feira):
-
Corretude de Algoritmo de Percurso em Profundidade:
============================================================ Algoritmo: possui_circuito Entrada: Um Grafo Direcionado G = (V,E). Saída: Um booleano. ------------------------------------------------------------ 01. PARA cada u ∈ V 02. | estado[u] := não_atingido 03. PARA cada u ∈ V 04. | SE estado[u] = não_atingido 05. | | SE possui_circuito_vértice(G,u) 06. | | | RETORNE verdadeiro. 07. RETORNE falso. ============================================================ ============================================================ Algoritmo: possui_circuito_vértice Entrada: Um Grafo Direcionado G = (V,E), um vértice "u". Saída: Um booleano. ------------------------------------------------------------ 01. estado[u] := atingido 02. PARA cada v ∈ N(u) 03. | SE estado[v] = não_atingido 04. | | SE possui_circuito_vértice(G,v) 05. | | | RETORNE verdadeiro. 06. | SENÃO 07. | | SE estado[v] = atingido 08. | | | RETORNE verdadeiro. 09. estado[u] := terminado 10. RETORNE falso. ============================================================
-
Tópicos da Argumentação:
-
Pré-Condições de possui_circuito_vértice:
-
∀x ∈ V, se estado[x] = atingido, então há um caminho de "x" a "u" em G.
-
estado[u] = não_atingido.
-
-
Pós-Condições de possui_circuito_vértice:
-
Se o retorno da função é verdadeiro, então há um circuito em G. (Não foi escrita, mas é essencialmente o que foi argumentado na 1ª parte da prova.)
-
O estado de vértices "atingidos" ou "terminados" não é alterado.
-
Se o estado de um vértice é "não_atingido" no início da chamada e é diferente ao final da chamada, então ele mudou para "terminado".
-
Se o retorno da função é falso, então "u" está "terminado".
-
Todo vértice "terminado" não participa de um circuito em G.
-
Se x,y ∈ V, existe um caminho de "x" a "y" e "x" está "terminado", então "y" também está "terminado" (mencionada na 2ª parte da argumentação).
-
-
OBSERVAÇÕES:
-
Para provar uma pós-condição, você deve considerar uma chamada qualquer da função, supor que as pré-condições são válidas no início da chamada e argumentar que a pós-condição será válida ao final da chamada ("contrato").
-
Você também pode supor que todas as pós-condições são válidas ao fim de uma chamada recursiva, mas deve provar que as pré-condições dessa chamada são válidas logo antes da chamada.
-
Por falta de tempo, foi falado apenas muito rapidamente sobre provas de terminação, embora o argumento seja fácil no caso dos algoritmos acima.
EXERCÍCIOS ESSENCIAIS:
-
Prove a pós-condição 6 acima.
Prove a pós-condição 5 acima (argumentação verbal feita em sala).
EXERCÍCIOS ADICIONAIS:
-
Prove a pós-condição 3 acima.
-
Prove a pós-condição 1 acima (argumentação verbal feita em sala).
MATERIAIS DE ESTUDO:
-
No Cormen, a corretude do Percurso em Profundidade é apresentada, em formato diferente, na seção 22.3 e no Lema 22.11 da seção 22.4.
-
-
Aula 10 (2016-09-21, Quarta-feira):
-
Tempo da Detecção de Ciclos via Busca em Largura: O(n).
-
Tempo de Execução da Busca em Profundidade (Detecção de Circuitos): O(n + m).
-
Definição de Ordenação Topológica e Relação com Circuitos num Grafo.
-
Escrita de Algoritmos O(n+m) para Ordenação Topológica:
-
Do início para o fim da ordenação: pelos vértices de grau de entrada igual a 0.
-
Do fim para o início da ordenação: pelos tempos de término da Busca em Profundidade.
-
EXERCÍCIOS ESSENCIAIS:
-
Exiba uma classe de grafos direcionados para a qual o algoritmo de detecção de circuitos execute em tempo ω(|V|) – isto é, para a qual o algoritmo não executa em tempo O(|V|).
-
Prove que, para todo grafo direcionado G = (V,E), se G não possui circuitos e possui pelo menos um vértice, então G possui um vértice no qual não chegam arestas. (A ideia da prova foi explicada em sala.)
EXERCÍCIOS ADICIONAIS:
-
Escreva um algoritmo O(|V| + |E|) que, ao invés de computar uma ordenação topológica do grafo de entrada G = (V,E), divida os vértices em "camadas":
-
Os vértices da camada 0 são aqueles nos quais não chegam arestas;
-
Os vértices da camada 1 são aqueles nos quais chegam arestas, mas apenas de vértices da camada 0;
-
Os vértices da camada 2 são aqueles nos quais chegam arestas, mas apenas de vértices das camadas 1 e 2; etc.
-
-
Escolha um dos algoritmos vistos em sala e prove que ele está correto. Se você escolher o primeiro, que é iterativo, então o cerne da prova consistirá em encontrar invariantes de laço adequados. Se você escolher o segundo, que é recursivo, então o cerne será encontrar pós-condições adequadas.
MATERIAIS DE ESTUDO:
-
No Cormen, o assunto Ordenação Topológica é apresentado na seção 22.4.
-
-
Aula 11 (2016-09-28, Quarta-feira):
-
Definição do Problema da Árvore Geradora Mínima (AGM).
-
Ideias de Solução para o Problema.
-
Estratégia Sugerida pela Turma: "enquanto G possuir ciclos, remova a aresta mais pesada de algum ciclo".
-
Prova do Argumento Essencial da Corretude da Estratégia Acima:
Seja G = (V,E) um grafo não-direcionado conexo cujas arestas têm os pesos de w : E → R. Seja também A ⊆ E tal que existe uma AGM T = (V,B) de G tal que B ⊆ A. Finalmente, seja e = {x,y} a aresta mais pesada de um ciclo C de G[A] (nesse caso, G[A] = (V,A)), e seja A' = A \ {e}. Então existe uma AGM T' = (V,B') de G tal que B' ⊆ A'.
EXERCÍCIOS ESSENCIAIS:
-
Escreva um algoritmo que materialize a estratégia discutida em sala. Qual é a complexidade do tempo de execução do seu algoritmo?
-
Utilizando o teorema provado em sala, prove que este algoritmo sempre retorna uma AGM de G:
========================================================= Algoritmo: AlgConceitual Entrada: G = (V,E) e "w". Saída: um grafo não-direcionado ponderado. --------------------------------------------------------- 1. ENQUANTO G possui ciclos 2. | Seja C um ciclo qualquer de G 3. | Remova de G a aresta mais pesada de C (ou "uma das") 4. RETORNE (G,w). =========================================================
EXERCÍCIOS ADICIONAIS:
-
A estratégia inversa àquela discutida em sala é: "começando sem nenhuma aresta, enquanto houver duas ou mais componentes conexas, adicione a aresta mais leve que não gera ciclos".
Assim sendo, utilizando a ideia de prova ilustrada em sala, prove que essa estratégia também sempre leva a uma AGM.
-
Escreva um algoritmo que materialize a estratégia do exercício anterior. Qual o tempo de execução dele?
MATERIAIS DE ESTUDO:
-
No Cormen, o problema da AGM é apresentado no capítulo 23.
-
-
Aula 12 (2016-10-03, Segunda-feira):
-
Tempo da Estratégia para Computação de AGM da Aula Anterior: O(m*n), sendo n = |V| e m = |E|.
-
Ideia inversa: "começando sem nenhuma aresta, enquanto houver duas ou mais componentes conexas, adicione a aresta mais leve que não gera ciclos".
-
Tempo dessa Estratégia com Busca Linear pela Aresta Leve: O(m*m).
-
Tempo dessa Estratégia com Ordenação ou Heap: O(m*lg(n) + m*n) (ordenação + checagem de ciclos).
-
Tempo dessa Estratégia com Componentes Conexas via Listas (Algoritmo de Kruskal): O(m*lg n).
EXERCÍCIOS ESSENCIAIS:
-
Escreva uma versão detalhada do algoritmo de Kruskal, na qual as arestas são ordenadas por peso no início do algoritmo, e na qual as componentes conexas do grafo construído são mantidas por meio de listas encadeadas. Use a heurística de "união ponderada" para Conjuntos Disjuntos (incluir os elementos da componente menor na componente maior).
-
Escreva uma variação do algoritmo da questão anterior, na qual, ao invés de se ordenar as arestas no início do algoritmo, se utiliza um "heap", no qual as arestas são inicialmente inseridas e de onde elas são, em seguida, sucessivamente retiradas.
EXERCÍCIOS ADICIONAIS:
-
Escreva um argumentação detalhada de que o Algoritmo de Kruskal executa em tempo O(m*lg n). Você provavelmente desejará usar o teorema 21.1 do Cormen ou o lema 3 do material [1] abaixo.
-
Em sala nós mencionamos que as componentes conexas do algoritmo de Kruskal também podem ser gerenciadas por meio da estrutura de Floresta para Conjuntos Disjuntos. Escreva uma variação de Kruskal que explicite o uso dessa estrutura.
MATERIAIS DE ESTUDO:
-
No Cormen, o Algoritmo de Kruskal é apresentado na seção 23.2, a estrutura de Conjuntos Disjuntos por Lista Encadeada na seção 21.2, e a estrutura de Floresta na seção 21.3.
-
A estrutura de Conjuntos Disjuntos por Lista Encadeada também está explicada nesta nota de aula [1], e a estrutura de Floresta nesta outra [2].
-
-
Aula 13 (2016-10-05, Quarta-feira):
-
Recapitulação da Estratégia do Algoritmo de Kruskal.
-
Discussão e Obtenção de uma Versão Detalhada do Algoritmo:
====================================================================== Algoritmo: Kruskal Entrada: grafo não-direcionado G = (V,E) e função w: E → R. Saída: grafo não-direcionado T. ---------------------------------------------------------------------- 01. Crie o grafo não-direcionado T = (V,∅) 02. PARA cada u ∈ V 03. | CC[u] := u 04. | tam[u] := 1 05. | lista[u] := criar_lista_vazia() 06. | insira_em(u, lista[u]) 07. Crie um heap H com as arestas de G, os pesos sendo as prioridades. 08. ENQUANTO T não possuir |V|−1 arestas 09. | {u,v} := extrair_mínimo(H) 10. | X := CC[u], Y := CC[v] 11. | SE X != Y 12. | | insira {u,v} em T 13. | | SE tam[X] < tam[Y] 14. | | | m := X, M := Y 15. | | SENÃO 16. | | | m := Y, M := X 17. | | PARA cada x ∈ lista[m] 18. | | | CC[x] := M 19. | | transfira os vértices de lista[m] para lista[M] 20. | | tam[M] := tam[M] + tam[m] 21. RETORNE T. ====================================================================== -
Discussão do Tempo O(m*lg n) do Algoritmo Acima, sendo n = |V| e m = |E|.
EXERCÍCIOS ESSENCIAIS:
-
Escreva uma versão ainda mais detalhada do Algoritmo de Kruskal, supondo que o grafo está representado por Listas de Adjacência.
Em particular, o seu algoritmo deve detalhar a implementação das linhas 1 (criação de T), 7 (percurso das arestas para a criação de H), 8 (condição de parada do laço principal), 9 (obtenção da aresta mais leve) e 12 (inserção da aresta em T) do algoritmo acima.
-
Argumente que, para qualquer vértice u ∈ V, o algoritmo acima realiza no máximo 2⌊lg(n)⌋ + 1 atribuições a CC[u].
DICA: há um limite inferior para o número de elementos da componente conexa de "u" após "k" atribuições a CC[u]?
EXERCÍCIOS ADICIONAIS:
-
Considere a variação do algoritmo acima na qual são removidas as linhas 13, 15 e 16, isto é, na qual sempre
m := XeM := Y. Descreva então um tipo de entrada para a qual essa variação sempre executa em tempo ϴ(n²). -
As 2 estratégias para obtenção de árvore geradora mínima que vimos em sala não são as únicas existentes. Considere, por exemplo, que, dado um grafo G, nós desejamos começar a construção de uma AGM a partir de um vértice "u", sempre mantendo conexo o grafo que está sendo construído. Como isso pode ser feito, e em que complexidade de tempo de execução?
MATERIAIS DE ESTUDO:
-
No Cormen, o Algoritmo de Kruskal é apresentado na seção 23.2, e a estrutura de Conjuntos Disjuntos por Lista Encadeada na seção 21.2.
-
A estrutura de Conjuntos Disjuntos por Lista Encadeada também está explicada nesta nota de aula [1].
-
-
Aula 14 (2016-10-10, Segunda-feira):
-
Discussão Detalhada do Tempo de Execução do Algoritmo de Kruskal.
-
Discussão e Exemplificação de Estratégia Alternativa para AGM (Prim).
-
Enunciado e Justificação Oral de Teorema para Corretude da Estratégia de Prim:
TEOREMA: Sejam
- G = (V,E) um grafo não-direcionado conexo.
- w : E → R.
- X ⊆ V, Y = V \ X e r ∈ X.
- A ⊆ E tal que:
- G[A] é conexo.
- X possui "r", os vértices de G[A] e nenhum outro.
- Existe uma AGM T = (V,B) de G tal que A ⊆ B.
- e = {u,v} uma aresta de peso mínimo dentre aquelas que "ligam" X e Y.
- A' = A ∪ {e}.
EXERCÍCIOS ESSENCIAIS:
-
Em sala, nós fornecemos a ideia da prova do teorema acima (que é semelhante à da prova de Kruskal). Escreva então a prova em detalhes.
-
Escreva o algoritmo de Prim em pseudocódigo.
EXERCÍCIOS ADICIONAIS:
-
Qual é o tempo de execução do algoritmo que você escreveu para a questão acima? Argumente detalhadamente.
-
(Cormen 23.2-2) Suponha que o grafo de entrada do algoritmo de Prim está armazenado em uma matriz de adjacência. Apresente uma implementação simples do algoritmo que execute em O(n²).
MATERIAIS DE ESTUDO:
-
No Cormen, o Algoritmo de Prim é apresentado na seção 23.2.
-
-
Aula 15 (2016-10-17, Segunda-feira):
-
Recapitulação da Estratégia do Algoritmo de Prim.
-
Conceitos de "Corte" e "Aresta Leve".
-
Discussão sobre como Materializar a Estratégia em Questão.
-
Escrita de 2 Versões do Algoritmo de Prim (Orientadas a Arestas e a Vértices):
====================================================================== Algoritmo: Prim_Arestas Entrada: Grafo não-direcionado G = (V,E), w : E → R, r ∈ V. Saída: Grafo não-direcionado. ---------------------------------------------------------------------- 01. T := ({r},∅) 02. PARA cada u ∈ V 03. | está_em_X[u] := falso 04. está_em_X[r] := verdadeiro 05. tam_X := 1 06. H := criar_heap_vazio() 07. PARA cada v ∈ N(r) 08. | insira_em({r,v}, w({r,v}), H) 09. ENQUANTO tam_X < |V| 10. | {u,v} := extrair_mín_de(H) 11. | SE ¬está_em_X[u] OU ¬está_em_X[v] 12. | | Insira a aresta {u,v} em T 13. | | SE ¬está_em_X[u] 14. | | | i := u 15. | | SENÃO 16. | | | i := v 17. | | está_em_X[i] := verdadeiro 18. | | ++tam_X 19. | | PARA cada j ∈ N(i) 20. | | | SE ¬está_em_X[j] 21. | | | | insira_em({i,j}, w({i,j}), H) 22. RETORNE T. ====================================================================== ====================================================================== Algoritmo: Prim_Vértices Entrada: Grafo não-direcionado G = (V,E), w : E → R, r ∈ V. Saída: Grafo não-direcionado. ---------------------------------------------------------------------- 01. T := ({r},∅) 02. PARA cada u ∈ V 03. | peso[u] := infinito 04. | está_em_X[u] := falso 05. peso[r] := 0 06. Crie um heap H com os elementos de V, a chave sendo o "peso". 07. ENQUANTO ¬está_vazio(H) 08. | u := extrair_mín_de(H) 09. | está_em_X[u] := verdadeiro 10. | SE u != r 11. | | Insira a aresta {u, pai[u]} em T 12. | PARA cada v ∈ N(u) 13. | | SE ¬está_em_X[v] E w({u,v}) < peso[v] 14. | | | peso[v] := w({u,v}) 15. | | | pai[v] := u 16. | | | subir_em(v, peso[v], H) // Manter Vetor de Posições no Heap 17. RETORNE T. ======================================================================
EXERCÍCIOS ESSENCIAIS:
-
Calcule a complexidade assintótica do tempo de execução dos algoritmos acima.
-
Escreva em pseudocódigo uma implementação de heap (binário) de mínimo que possua pelo menos as funções utilizadas acima:
-
criar_heap_vazio()
-
inserir_em(x, c, H): insere o elemento "x" com chave "c" em H.
-
extrair_mín_de(H): remove e retorna o mínimo de H (atualiza H).
-
criar_heap(H, n): permuta os "n" elementos do vetor H transformando-o num heap.
-
subir_em(x, c, H): diminui a chave do elemento "x" para o valor "c", atualizando H.
-
EXERCÍCIOS ADICIONAIS:
-
(Cormen 23.2-5) Suponha que, no grafo de entrada do algoritmo de Prim, os pesos de todas as arestas são inteiros de 1 a W (W é dado como entrada). Escreva uma versão do algoritmo que se beneficia desse fato. Qual é o tempo de execução dessa versão?
-
(Cormen 23.2-7) Suponha que um grafo G já tem uma AGM computada. Quanto tempo leva para atualizar a árvore se adicionarmos a G um novo vértice e as respectivas arestas?
MATERIAIS DE ESTUDO:
-
No Cormen, o Algoritmo de Prim é apresentado na seção 23.2.
-
-
Aula 16 (2016-10-19, Quarta-feira):
- Implementação: Computar AGM.
INSTRUÇÕES PRELIMINARES:
-
O sistema operacional e a linguagem de programação ficam à sua escolha. A minha sugestão, porém, é o sistema Ubuntu e a linguagem C, que eu sempre utilizo e portanto poderei explicar com facilidade.
-
Mantenha sempre em mente que o objetivo da aula é concluir as tarefas propostas, e que isso deve ser feito durante o tempo de aula. Assim, seja objetivo ao programar: prefira soluções simples e faça pouco tratamento de erros, lembrando que você pode refinar o seu código depois da aula se assim desejar.
-
Eu estarei à disposição para ajudar: tire as suas dúvidas rapidamente, mesmo que sejam trivialidades de programação cuja solução você não esteja lembrando.
-
Computar AGM
-
TAREFA: Escreva um programa que determine, para cada grafo de entrada desta questão, uma AGM do grafo, e que então compare as respostas obtidas com as soluções aqui fornecidas.
-
ENTRADA: neste arquivo (são 140 grafos e o relatório de geração), no mesmo formato combinado anteriormente, COM A ADIÇÃO DE UM PESO RACIONAL PARA CADA ARESTA.
-
SOLUÇÕES: neste arquivo, no seguinte formato:
-
A primeira linha dá o peso da AGM. Exemplo: "-579.9 (peso da AGM)".
-
As outras n−1 linhas dão as arestas da árvore. Exemplo: "2 3".
-
-
-
Aula 17 (2016-10-26, Quarta-feira):
-
O Problema de Caminhos Mínimos em Grafos Ponderados.
-
Discussão sobre como Resolver o Problema.
-
Ilustração da Estratégia do Algoritmo de Dijkstra para uma Instância Concreta.
EXERCÍCIOS ESSENCIAIS:
-
Se os pesos das arestas da entrada do algoritmo de Dijkstra forem todos 1, os vértices são visitados em alguma ordem familiar?
-
Escreva um algoritmo que materialize a estratégia discutida em sala.
EXERCÍCIOS ADICIONAIS:
-
Demonstre, por meio de um exemplo, que a árvore de caminhos mínimos não necessariamente é uma árvore geradora mínima, e vice-versa.
-
A estratégia para a obtenção de caminhos mínimos discutida em sala foi apresentada no contexto de grafos não-direcionados. Alguma mudança é necessária no caso de grafos direcionados?
MATERIAIS DE ESTUDO:
-
No Cormen, o Algoritmo de Dijkstra é apresentado na seção 24.3, que depende do conteúdo apresentado antes da seção 24.1.
-
-
Aula 18 (2016-10-31, Segunda-feira):
-
Recapitulação da Estratégia do Algoritmo de Dijkstra.
-
Construção do Algoritmo de Dijkstra (versão com Heap).
-
Prova da Corretude do Algoritmo, na forma deste resultado:
TEOREMA: Sejam:
- G = (V,E) um grafo não-direcionado ponderado por w : E → Reais+,
- o ∈ V,
- S ⊆ V tal que
- o ∈ S,
- R ≠ ∅, sendo R = V \ S, e
- δ(o,u) ≠ infinito, para todo u ∈ S.
- Para todo v ∈ R,
- e[v] = infinito, se ∄u ∈ S ∩ N(v).
- e[v] = mín{ δ(o,u) + w({u,v}) : u ∈ S ∩ N(v) }, em c.c..
- D = mín{ e[v] : v ∈ R },
- w ∈ R tal que e[w] = D.
Assim sendo, e[w] = δ(o,w).
EXERCÍCIOS ESSENCIAIS:
-
O algoritmo de Dijkstra ainda funciona se os pesos das arestas puderem ser negativos? Se sim, algo muda na prova do teorema acima? Se não, qual parte da prova não funciona mais?
-
Escreva uma versão do algoritmo de Dijkstra que utilize um vetor ao invés de um heap.
EXERCÍCIOS ADICIONAIS:
-
Qual é a complexidade do tempo de execução do algoritmo escrito em sala? E da versão que utiliza vetor ao invés de heap (exercício acima)?
-
Como o teorema acima se relaciona com a corretude do algoritmo de Dijkstra? Enuncie invariantes de laço que impliquem na corretude do algoritmo, e prove-os por meio do teorema acima.
MATERIAIS DE ESTUDO:
-
No Cormen, o Algoritmo de Dijkstra é apresentado na seção 24.3, onde a corretude dele também é provada, com base em lemas demonstrados na seção 24.5.
-
-
Aula 19 (2016-11-07, Segunda-feira):
-
Complexidade do Tempo de Execução do Algoritmo de Dijkstra.
-
Observação do Algoritmo de Dijkstra em Grafos com Pesos Negativos.
-
Ideia, Pseudocódigo e Complexidade do Algoritmo de Bellman-Ford.
EXERCÍCIOS ESSENCIAIS:
-
Suponha que um certo grafo não possui ciclos de peso negativo; por que o algoritmo de Bellman-Ford não retornará falso para esse grafo? E por que retornaria falso se o grafo possuísse um ciclo negativo?
-
Suponha que, numa iteração "i = k" do laço principal algoritmo de Bellman-Ford, nenhum vértice teve o campo "d" alterado; é necessário realizar as demais iterações do laço?
EXERCÍCIOS ADICIONAIS:
-
Suponha que, dados um grafo G e um vértice "o" de origem, nós desejamos não apenas obter um caminho de peso mínimo de "o" a cada v ∈ V, mas que desejamos também que, para cada vértice "v", o caminho até "v" tenha o menor número de arestas possível, dentre todos os caminhos de peso mínimo de "o" a "v". Que alterações é então necessário fazer no algoritmo de Dijkstra? E no algoritmo de Bellman-Ford?
-
(Cormen, 24.1-4) Modifique o algoritmo de Bellman-Ford de forma que ele identifique todos os vértices que participam de ciclos negativos (por exemplo fazendo d[v] = −∞).
MATERIAIS DE ESTUDO:
-
No Cormen, o Algoritmo de Bellman-Ford é apresentado na seção 24.1.
-
-
Aula 20 (2016-11-09, Quarta-feira):
-
Recapitulação do Algoritmo de Bellman-Ford.
-
Demonstração deste Teorema:
O algoritmo de Bellman-Ford retorna verdadeiro sse não há circuitos de peso negativo no grafo de entrada.
-
Algoritmo Linear para Obtenção de Caminhos Mínimos em Grafos sem Circuitos (DAGs).
EXERCÍCIOS ESSENCIAIS:
-
Crie um grafo direcionado sem circuito de pelo menos 7 vértices e 13 arestas, e execute sobre ele os 3 algoritmos de caminhos mínimos que estudamos.
-
O algoritmo de caminhos mínimos para DAGs escrito em sala recebe um grafo G e uma origem "o", e então calcula uma ordenação topológica de G. Entretanto, dado que apenas as distâncias a partir de "u" são necessárias, o algoritmo poderia calcular uma ordenação topológica de uma parte menor do grafo, não é verdade?
Com base nessa observação, escreva então uma versão melhorada do algoritmo. Além disso: qual é o tempo de execução dessa nova versão, no pior caso?
EXERCÍCIOS ADICIONAIS:
-
(Cormen, 24.2-4) Escreva um algoritmo eficiente para contar o número total de caminhos em um DAG (grafo direcionado sem circuito). Argumente a corretude e o tempo de execução do algoritmo.
-
Construa um grafo direcionado para o qual o algoritmo de Dijkstra funciona e o algoritmo para grafos sem circuitos não funciona, e mostre o que acontece de errado.
Idem para os algoritmos de Bellman-Ford e Dijkstra, respectivamente.
MATERIAIS DE ESTUDO:
-
No Cormen, Caminhos Mínimos em Grafos sem Circuitos são estudados em §24.2.
-
-
Aula 21 (2016-11-12, Sábado):
- Implementação: Computar Caminhos Mínimos.
INSTRUÇÕES PRELIMINARES:
-
O sistema operacional e a linguagem de programação ficam à sua escolha. A minha sugestão, porém, é o sistema Ubuntu e a linguagem C, que eu sempre utilizo e portanto poderei explicar com facilidade.
-
Mantenha sempre em mente que o objetivo da aula é concluir as tarefas propostas, e que isso deve ser feito durante o tempo de aula. Assim, seja objetivo ao programar: prefira soluções simples e faça pouco tratamento de erros, lembrando que você pode refinar o seu código depois da aula se assim desejar.
-
Eu estarei à disposição para ajudar: tire as suas dúvidas rapidamente, mesmo que sejam trivialidades de programação cuja solução você não esteja lembrando.
INSTRUÇÕES:
-
TAREFA: Escreva um programa que determine, para cada grafo de entrada desta questão, as distâncias e caminhos mínimos a partir do vértice de menor índice. Os grafos de entrada são direcionados; alguns deles têm arestas de peso negativo, outros não.
SUGESTÃO: comece implementando o algoritmo mais simples, mas em seguida implemente os demais. Quando todos estiverem implementados, aplique sempre o mais rápido, de acordo com as propriedades de cada grafo.
-
ENTRADA: neste arquivo (são 200 grafos e o relatório de geração), no mesmo formato combinado anteriormente, COM A ADIÇÃO de um peso racional para cada aresta.
-
SOLUÇÕES: neste arquivo, no seguinte formato:
-
Primeira linha: "
1 (Sem Circuitos Negativos)" ou "0 (Há Circuitos Negativos)". -
Caso não haja circuitos de peso negativo, as demais linhas dão as distâncias do primeiro vértice aos demais, além de um caminho mínimo, caso exista um (os vértices estão numerados a partir de 1, por homogeneidade com os arquivos de entrada). Exemplo:
v: 1 dist: 0 caminho: 1 v: 2 dist: 93.2 caminho: 1 2 v: 3 dist: 141.7 caminho: 1 2 4 3 v: 4 dist: 132.6 caminho: 1 2 4 v: 5 dist: INFINITO
-
-
Aula 22 (2017-01-11, Quarta-feira):
-
Introdução Informal ao Problema de Fluxo em Grafos.
-
Discussão sobre Como Resolver o Problema.
-
Intuição do Método de Ford-Fulkerson e Aplicação em Exemplos.
EXERCÍCIOS ESSENCIAIS:
-
Suponha que a entrada para o problema de fluxo seja dada na forma de um grafo direcionado G = (V,E), vértices s,t ∈ V (origem e destino) e uma função c : E → R+.
Nesse caso, um fluxo poderia ser definido como uma função f : E → R+ sujeita às restrições comentadas na aula:
-
Capacidade: o fluxo numa aresta não pode exceder a capacidade desta.
-
Conservação: o fluxo chegando num vértice deve ser igual ao fluxo saindo dele.
Assim sendo, FORMALIZE AS RESTRIÇÕES ACIMA.
-
-
Considere a seguinte rede de fluxo, sendo 0 o vértice de origem e 4 o vértice de destino:
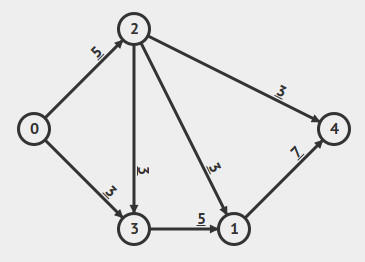
Assim sendo:
-
Simule uma execução do Método de Ford-Fulkerson na qual o primeiro caminho encontrado é "0, 2, 4".
-
Simule uma execução do Método de Ford-Fulkerson na qual o primeiro caminho encontrado é "0, 2, 1, 4".
-
EXERCÍCIOS ADICIONAIS:
-
Considere a seguinte rede de fluxo, sendo 0 o vértice de origem e 3 o vértice de destino:
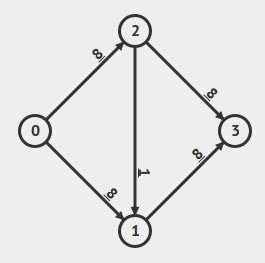
Assim sendo:
-
Qual é o número mínimo de iterações realizadas pelo Método de Ford-Fulkerson para a rede acima? Explicite os caminhos encontrados.
-
E o número máximo de iterações? Explicite os caminhos encontrados.
-
-
Considere a variação do problema de fluxo na qual, ao invés de apenas um vértice de origem e um vértice de destino, há vários vértices de origem (s1, ..., sx) e vários vértices de destino (t1, ..., ty). Mostre como resolver essa versão do problema.
MATERIAIS DE ESTUDO:
-
No Cormen, o Problema de Fluxo é introduzido em §26.1 e o Método de Ford-Fulkerson em §26.2.
-
-
Aula 23 (2017-01-16, Segunda-feira):
-
Recapitulação Informal do Problema de Fluxo e do Método de Ford-Fulkerson.
-
Definição Formal do Problema de Fluxo.
-
Definição de Soma Implícita e Prova de que f(s,V) = f(V,t).
-
Definição de Capacidade Residual (cf), Rede Residual (Gf), Caminho Aumentante, Fluxo Induzido por Caminho Aumentante (fp).
EXERCÍCIOS ESSENCIAIS:
-
(Cormen 2ª Edição, Lema 26.1) Prove que, se "f" é um fluxo numa rede G = (V,E,s,t,c), então:
-
f(X,X) = 0, ∀X ⊆ V.
-
f(X,Y) = −f(Y,X), ∀X,Y ⊆ V.
-
[ X ∩ Y = ∅ → f(X U Y, Z) = f(X,Z) + f(Y,Z) ], ∀X,Y,Z ⊆ V .
-
-
(Cormen 2ª Edição, Lema 26.2) Mostre que, se "f" é um fluxo numa rede G = (V,E,s,t,c), e se f' é um fluxo na rede residual Gf, então a função g = f + f' é também um fluxo em G, e |g| = |f| + |f'|.
EXERCÍCIOS ADICIONAIS:
-
(Cormen 2ª Edição, Exercício 26.1-6) Se f e f' são fluxos numa rede G = (V,E,s,t,c), então a função g = f + f' é necessariamente também um fluxo em G? Das 3 propriedades da definição de fluxo, quais são necessariamente satisfeitas por "g", e quais podem não sê-lo?
-
Prove que, se "f" é um fluxo numa rede G = (V,E,s,t,c) e a rede residual Gf possui um caminho aumentante, então existe um fluxo f' tal que |f'| > |f|.
MATERIAIS DE ESTUDO:
-
Cormen, seções 26.1 e 26.2.
-
-
Aula 24 (2017-01-18, Quarta-feira):
-
Recapitulação de Ford-Fulkerson e Resultados Associados.
-
Definição de Corte e a Capacidade Correspondente.
-
Prova dos Lemas "|f| = f(S,T)" e "f(S,T) ≤ c(S,T)".
-
Prova do Teorema: "Se f é máximo, então ∃(S,T) tal que |f| = c(S,T)".
-
Pseudocódigo e Complexidade de Ford-Fulkerson para Capacidades Racionais e Inteiras.
EXERCÍCIOS ESSENCIAIS:
-
Prove que, para quaisquer fluxo "f" e corte (S,T), se |f| = c(S,T), então "f" tem valor máximo e (S,T) tem capacidade mínima.
-
Escreva uma prova precisa de que, se uma rede tem capacidades inteiras, então o método de Ford-Fulkerson termina e retorna um fluxo também inteiro.
EXERCÍCIOS ADICIONAIS:
-
(Cormen 2ª Edição, 26.2-8) Mostre que, para toda rede G = (V,E,s,t,c), existe uma sequência de no máximo |E| caminhos aumentantes que leva a um fluxo máximo.
-
Prove ou Refute: se uma execução de Ford-Fulkerson termina após K caminhos aumentantes, então uma aresta (u,v) pode ter ficado saturada no máximo ⌈K/2⌉ vezes.
MATERIAIS DE ESTUDO:
-
A Wikipédia traz um exemplo de execução infinita de Ford-Fulkerson num grafo com apenas 6 vértices, e o artigo científico correspondente traz outros exemplos.
-
Cormen, seções 26.1 e 26.2.
-
-
Aula 25 (2017-01-23, Segunda-feira):
-
Recapitulação de Ford-Fulkerson e Resultados Associados.
-
Prova de que, ∀v, δf(s,v) é Não-Decrescente (sobre f) em Edmonds-Karp.
-
Argumentação de que Edmonds-Karp sempre Executa O(n*m) Iterações.
-
Explicação do Tempo O(n*m²) do Algoritmo de Edmonds-Karp.
EXERCÍCIOS ESSENCIAIS:
-
Prove por escrito este resultado argumentado oralmente em sala: se
-
p e p' são caminhos aumentantes utilizados numa execução de Edmonds-Karp, o primeiro sendo anterior ao segundo;
-
Gf e Gf' são, respectivamente, redes residuais onde p e p' se encontram;
-
(u,v) é crítica tanto em p quanto em p',
-
-
Com base no resultado anterior, escreva uma prova de que Edmonds-Karp sempre executa O(n*m) iterações.
EXERCÍCIOS ADICIONAIS:
-
(Cormen 2ª Edição, 26.2-4) Prove ou Refute: para quaisquer rede G, fluxo f em G e vértices u,v de G, cf(u,v) + cf(v,u) = c(u,v) + c(v,u).
-
Como sabemos, o problema de caminhos mínimos pode ser resolvido mais rapidamente no caso particular de grafos sem circuitos: basta relaxar as arestas seguindo uma ordenação topológica. E no problema de fluxo, essa estratégia também funciona? Se sim, como? Se não, por que razão?
MATERIAIS DE ESTUDO:
-
Cormen, seção 26.2.
-
-
Aula 26 (2017-01-25, Quarta-feira):
-
Introdução ao Problema de Emparelhamento Máximo em Grafos Bipartidos.
-
Redução do Problema de Emparelhamento ao Problema de Fluxo.
-
Argumentação da Corretude e da Complexidade de Tempo do Algoritmo.
EXERCÍCIOS ESSENCIAIS:
-
Escreva detalhadamente a definição da rede de fluxo correspondente a uma entrada G = (V,E) para o problema de emparelhamento.
-
Escreva em detalhes uma prova de que o algoritmo de emparelhamento via fluxo executa em tempo O(n*m).
EXERCÍCIOS ADICIONAIS:
-
Se M é um emparelhamento em G = (V,E), qual é a definição precisa do fluxo correspondente?
-
Escreva em detalhes uma prova de que o emparelhamento induzido por um fluxo máximo é também máximo.
MATERIAIS DE ESTUDO:
-
Cormen, seção 26.3.
-
-
Aula 27 (2017-01-30, Segunda-feira):
- Implementação: Computar Fluxo Máximo.
INSTRUÇÕES PRELIMINARES:
-
O sistema operacional e a linguagem de programação ficam à sua escolha. A minha sugestão, porém, é o sistema Ubuntu e a linguagem C, que eu sempre utilizo e portanto poderei explicar com facilidade.
-
Mantenha sempre em mente que o objetivo da aula é concluir as tarefas propostas, e que isso deve ser feito durante o tempo de aula. Assim, seja objetivo ao programar: prefira soluções simples e faça pouco tratamento de erros, lembrando que você pode refinar o seu código depois da aula se assim desejar.
-
Eu estarei à disposição para ajudar: tire as suas dúvidas rapidamente, mesmo que sejam trivialidades de programação cuja solução você não esteja lembrando.
INSTRUÇÕES:
-
TAREFA: Escreva um programa que determine, para cada grafo de entrada desta questão, os fluxos máximos a partir do vértice de menor índice – isto é, o fluxo máximo do vértice 1 ao vértice 2, o fluxo máximo do vértice 1 ao vértice 3, ..., o fluxo máximo do vértice 1 ao vértice "n". Os grafos de entrada são direcionados e as capacidades das arestas são números racionais.
-
ENTRADA: neste arquivo (são 200 grafos e o relatório de geração), no mesmo formato combinado anteriormente, com a adição de um peso racional para cada aresta.
-
SOLUÇÕES: neste arquivo, no seguinte formato (exemplo):
s: 1, t: 2, flow: 62.2 s: 1, t: 3, flow: 78.3 s: 1, t: 4, flow: 0 s: 1, t: 5, flow: 63.6